2020 Ai Tong School (ATS) P5 Math SA2 Examination Paper Analysis

Introduction

Do you spend too much time deciding how to solve P5 Fractions word problems?

In this blog post, we will be analysing a question on the topic of Fractions from the 2020 Ai Tong School (ATS) P5 Math SA2 Examination Paper.

By the end of this blog post, you will learn when to use the problem-solving technique, Numerator The Same Concept and how to use the Numerator The Same Concept!

Alternatively, you can watch our explainer video on this question here.

Let’s Take A Look At This Fractions Question

Source: Ai Tong School — 2020 P5 Math SA2 Examination Paper [Q7]

Identifying Keywords

Let us first identify the keywords in the question.

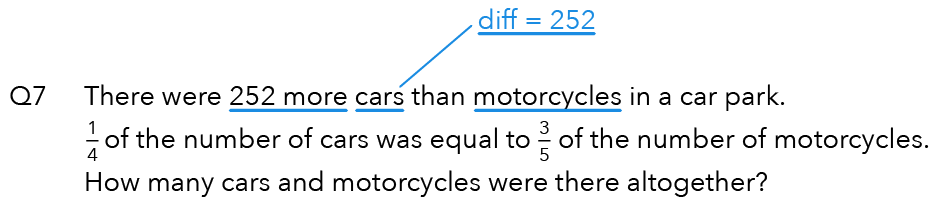
There were 252 more cars than motorcycles in the car park.

Do you think that car park is a keyword? No!

The car park is just a location for vehicles like cars and motorcycles to park in.

So what exactly are we comparing in this Fractions question? We’re comparing the number of cars and the number of motorcycles in the car park.

The phrase “252 more cars than motorcycles” tells us that there are 252 more cars compared to motorcycles.

Source: Ai Tong School — 2020 P5 Math SA2 Examination Paper [Q7]

The second sentence tells us that 1/4 of the number of cars was equal to 3/5 of the number of motorcycles.

Some of you have learned in school that whenever you see “one fraction of something is equal to another fraction of something else,” it is called the Equal Concept.

However, some of you may have also heard your teacher refer to this as the Numerator The Same Concept.

Solving Using The Numerator The Same Concept

🧐 What Is The Numerator The Same Concept? 🧐

Whenever we see that one fraction of something (in this case, the cars) is equal to another fraction of another item (in this case, the motorcycles) we are going to come up with an equation.

 

Now, let us look at the numerators and think about how we can make them the same number.

We have 1 on the first fraction and 3 on the second fraction.

How can we make the numerators 1 and 3 the same number?

The trick is to find their Lowest Common Multiple (LCM)!

🧐 What Is The Least Common Multiple (LCM)? 🧐

It is the smallest positive integer that is divisible by each of the given numbers without leaving a remainder.

Let’s list down their multiples:

Both of them have the number 3, so I am going to multiply our first numerator, 1, with 3.

🏅 Don’t Forget This After Finding The LCM 🏅

Once you have multiplied the LCM with your numerator, remember to do the same to your denominator.

Because we multiplied the numerator by 3, we are going to do the same with our denominator. Therefore, we are going to multiply the denominator 4 with 12 to get:

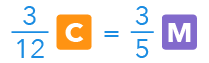
Now, we have the same numerators! But we are not yet done.

💡 What Do Denominators Of Fractions With The Same Numerator Tell Us? 💡

The denominator essentially tells us the total number of units that each vehicle has.

Let’s come up with a summary. Since the denominator of the cars is 12, it means that the cars have 12 units. Meanwhile, since the denominator of motorcycles is 5, the motorcycles have 5 units.

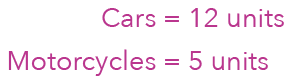
Now that we know the units, what do we do next?

Let us read the third sentence: “How many cars and motorcycles were there altogether?”

What is the difference between the units of cars and motorcycles?

Let us go back to our first sentence, which states that there were 252 more cars than motorcycles and we have not used this information yet.

The 7 units, which is the difference between the vehicles, correspond to the “252 more cars than motorcycles.”

Therefore, we can come up with an equation:

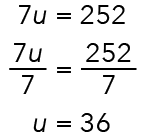
Now, when they get the value of the unit, many of my students would be so happy that they will write it down as the final answer.

However, this is wrong!

Why? Because if you read the question carefully, this is not what it is asking.

The question is asking how many cars and motorcycles were there altogether.

🤔 What Does ‘Altogether’ Mean? 🤔

Altogether means that we are looking for the total number of vehicles.

Have we found the total? No, we have not.

Going back to our solution, we already know the value of the unit, which is 36. But because we are looking for the total, we have to go back to the number of cars and motorcycles in terms of units.

Let us add the total units of each vehicle.

We already found the value of each unit, which is 36. So we can multiply 17 with 36 to get our final answer.

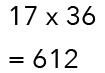
However, do we just write down 612 as our final answer?

Remember that the question is asking us about the total number of cars and motorcycles, which are vehicles.

Therefore, we should write down 612 vehicles as our final answer.

Final Answer

612 vehicles

Conclusion

I hope that after reading this P5 Fractions blog post, you have learned these key points:

• When you see “one fraction of something is equal to the fraction of another item,” you can use the Numerator The Same Concept.
• To make the numerators of 2 fractions the same, find their Lowest Common Multiple.
• Multiply the Lowest Common Multiple (LCM) to the numerator and then do the same to your denominator.
• The denominators will tell you the total units of each variable.

Stay tuned for more P5 Math word problems!