Introduction
Welcome back to another blog post on the topic of Fractions.
In this blog post, I will teach you how to solve P5 Math word problem sums by forming simultaneous equations. We will analyse a question from the 2018 Anglo-Chinese School (Primary) P5 SA1 Examination Paper.
Keep on reading if you want to learn an important tip to solve word problems involving Fractions faster!
You can also watch my explainer video for free by clicking the link.
Let’s Take A Look At This Fractions Question

Source: Anglo-Chinese School (Primary) – 2018 P5 SA1 Examination Paper [Q16]
Read Also:
Thought Process
Let us read the question. 240 pupils attended the Primary 5 Adventure Camp.
4/5 of the boys and 2/5 of the girls brought sleeping bags with them.
In this sentence, we see two fractions — 4/5 of the boys and 2/5 of the girls.
Are these two fractions referring to the same item? Is this an Equal Concept question where we could safely make either the numerator or the denominator the same to solve the question?
No, because 4/5 refers to boys only and 2/5 of the girls only.
Do we know the number of boys and the number of girls?
If we do not know, we cannot assume that there is an equal number of boys and girls. We also cannot assume and make the denominator the same since both the numbers of boys and girls are unknown.
Hence, to help us differentiate between the boys and girls, we need to assign a letter to solve the question.
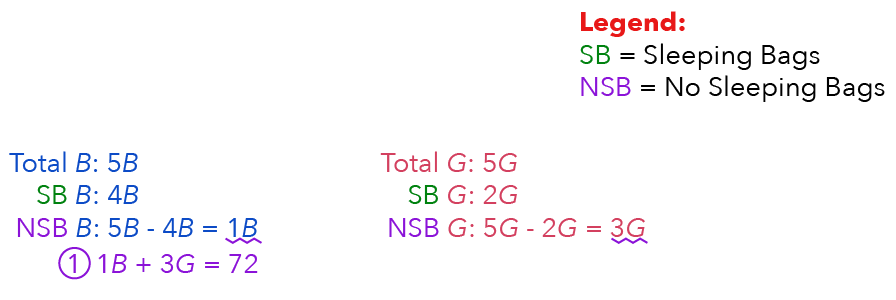
Separating the numerator from the denominator for boys, the denominator 5 tells us the total number of boys, which we can denote with 5B.

The numerator 4 tells us the number of boys with sleeping bags, so let’s use 4B to indicate the number of boys with sleeping bags.

What is left of 5B – 4B?
We get 1B, and this is the number of boys without sleeping bags.
Let’s note this down as 1B.

Can you do the same for the girls?
Separating the numerator from the denominator for the girls, the denominator 5 tells us the total number of girls, which we can denote with 5G.

The numerator 2 tells us the number of girls with sleeping bags with sleeping bags, so let’s use 2G to indicate the number of girls with sleeping bags.

What is left of 5G – 2G?
It will give us 3G, and this is the number of girls without sleeping bags.

Now that we are done, let’s continue reading.
72 pupils did not bring sleeping bags.
These 72 pupils are represented by 1B and 3G since they did not bring sleeping bags.
You can write this down as equation 1.
Can we form another equation?
Yes! The first sentence tells us that there were a total of 240 students, which comprises 5B and 5G.
So let’s write this down as equation 2.

This is a classical case of forming Simultaneous Equations to solve a question.
📝 How can we solve this question? 📝
When we want to solve for one letter (letter B in this case) we need to get rid of the other letter, which is letter G.
How we can remove G is to make sure that B in both equation 1 and equation 2 have the same quantity.

Since equation 2 has 5B, we can make B in equation 1 the same as equation 2 by simply multiplying equation 1 with the number 5.
This will give us:
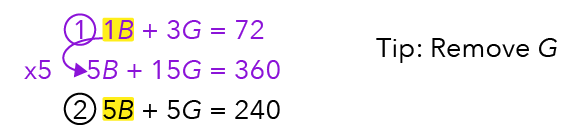
Now, let’s subtract the items in equation 1 from equation 2.
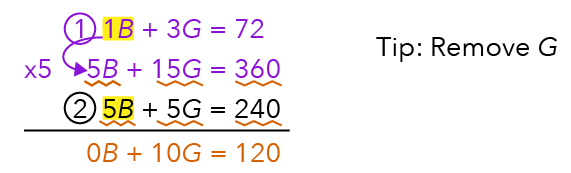
We now have 10G = 120.
Now, can you solve for 1G from here?
To get 1G, simply take 120 divided by 10.
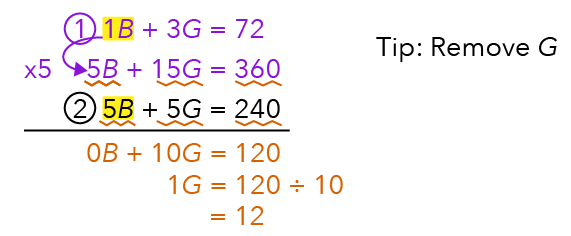
We now have 12.
How should we solve for B?
We can substitute what we have found for G into equation 1 to solve for B.
First, we will find 3G, which will give us 12 x 3 = 36.
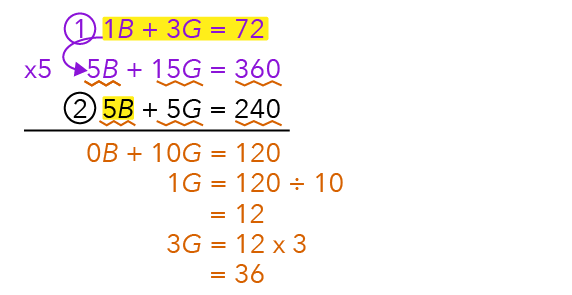
Using equation 1, let’s put all the known numbers in, and we’ll arrive at 1B + 36 = 72.
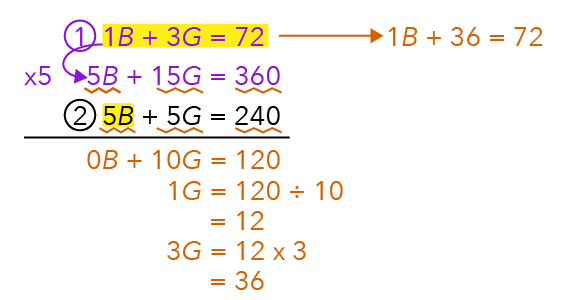
If you are unable to see how we can derive the answer for 1B, draw a simple model.
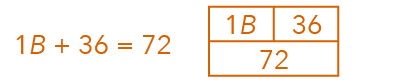
Let us now solve it.
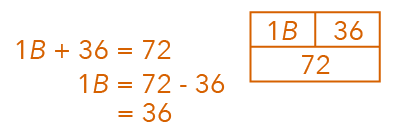
To find the total number of boys who attended the Primary 5 Adventure Camp, we need to find 5B.
So to find 5B, simply take 36 x 5.
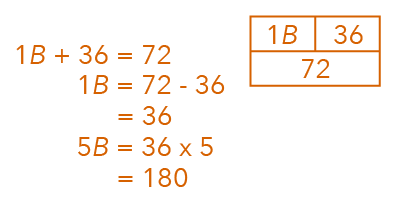
Suggested Answer For Q16
180 boys
Conclusion
I hope that after reading this P5 Math blog post, you learnt how to form simultaneous equations to solve questions involving Fractions.
Remember that when you need to solve for one letter — in this case the letter B — you need to get rid of the other letter (letter G) first!
Stay tuned for more P5 Math problem-solving techniques!

If you like our methodology, we've some ongoing weekly Math classes:








