Introduction
Welcome back to another Secondary 3 A-Math blog post!
If you are looking for tips to solving exponentials questions quicker and more accurately, keep on reading!
In this A-Math blog post, I will be discussing the Laws of Indices that you should apply when solving exponential functions.
You can also watch my explainer video on The Pique Lab’s YouTube channel for free by clicking this link.
Let’s Take A Look At This Exponentials Question

Source: Mayflower Secondary School — 2018 S3E SA1 Examination Paper [Q5(a)]
Read Also:
Thought Process
Where do we begin solving this?
The first question we must ask ourselves is whether the given terms share a common base.
Let us list the two bases in the equation.
They are 4 and 32.
The number 4 can be rewritten as the base term of 2 raised to the power of 2.
What about 32? Can it also be rewritten to a base 2 term? Yes, it can! It will be 2 to the power of 5.
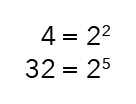
Next, let’s use this relationship to rewrite the given equation.
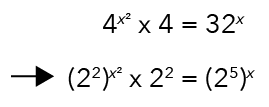
In this format, notice that there are two terms with brackets.
What Are The Laws Of Indices?
To remove these, we will use the Laws of Indices.
📕 What Are The Laws Of Indices? 📕
They are the rules when simplifying expressions involving powers of the same base.
The first law that we will be activating here is as follows:
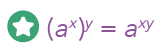
This law tells us that when we take the base term and raise it to two powers, first by x and then by y, we will simplify by multiplying their exponents.
Let us apply that to our equation.
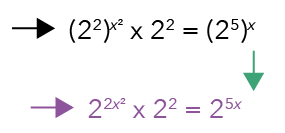
Notice that on the left-hand side, we have a product of two terms and these two terms share the same base.
This will activate our next Law of Indices:
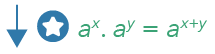
This law tells us that when we have a product of two terms that share the same base, we’ll simplify them by adding the exponents.
Let us apply this law to our equation on the left-hand side.
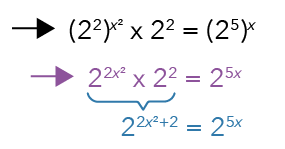
At this point, notice that the equation has been reduced to a point where there is only one term on each side of the equation.
These two terms have the same base.
If they are equal to one another, and they share the same base, what can we conclude about their corresponding powers? They will be the same. This is our next law of indices.

Hence, we will now extract an equation relating the two powers together.
Let’s shift the 5x over to the left side to attain this equation:
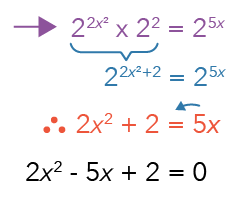
What do you notice?
This is the standard quadratic equation! We can now solve this equation by factorising the quadratic expression to obtain the final answer.
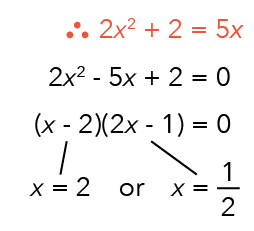
Suggested Answer
x = 2 or x 1/2
Conclusion
I hope that this blog post on how to use the Laws of Indices to solve exponential questions will help you do better in your A-Math examinations!
Remember to apply these laws when asked to solve exponential functions.

Stay tuned for more Secondary 3 A-Math blog posts coming your way!

If you like our methodology, we've some ongoing weekly Math classes:







