Beginner’s Guide To Cross Multiplication

Have you ever found yourself scratching your head when faced with fractions in Math problem sums? 

Don’t worry, you’re not alone! Fractions can be tricky to manipulate, especially when you’re trying to compare or solve equations involving them.

In the blog post, we discuss a handy technique that can solve your fraction-solving woes: cross multiplication.

Let me start with a little story time.

Once, I asked a student, “Do you know when you can use cross multiplication?” He replied, “When you see fractions! Like this…” He wrote the following on the board:

Another student overheard and said, “No, that’s not right!” He then wrote the following on the board:

Who do you think is correct?

In a way, both of them are right. We use cross multiplication when we see fractions. However, we can only use cross multiplication when we see “fraction = fraction”.

💡 What Is Cross Multiplication? 💡

Cross multiplication is a technique to solve equations involving algebraic fractions.

How Is Cross Multiplication Used?

Can you recall how cross multiplication works? If not, let me show you an easy way to remember!

That’s right! Use a butterfly 🦋

This is how it works. First, draw two loops as shown.

Next, we multiply the numbers in each loop.

Now, we solve  to get .

It’s always a good habit to check if our answer is correct. Do you know how to do that?

That’s right, substitute  into the original equation and check if the values on the left and right sides are the same.

Check:

LHS =  =  =  = RHS

Since the values on both sides are the same, our answer  is correct!

Why Does Cross Multiplication Work?

Let’s try to solve  in a different way.

Let’s make both sides of the equation have the same denominator.

Now that the denominators are the same, compare the numerators. What do you observe?

That’s right!  which is the same result we had when we did cross multiplication.

This is not sorcery!

What did we do to the left numerator? We multiplied by 3, which is also the right denominator.

What did we do to the right numerator? We multiplied by , which is also the left denominator.

So instead of doing this:

We do this:

Cross-multiplication speeds things up, don’t you think so?

Applying Cross Multiplication To The Algebraic Ratio Question

A student once asked me the following question:

Given that  and  .

(a) Find the value of   .

(b) Hence, find the value of   .

I can feel some of you cringing!

I feel you, so before I reveal the answer to you, let’s see how we can approach this problem using a similar and simpler problem.

Given  , find the value of   .

The Guess and Check Approach

Let’s try to guess the values of  and . We will use a table to help us to organise our guesses.

Now, we have to answer the question. Since  and , the value of is  is .

This is too time consuming.

Is there an easier way? Of course, there is!

The Cross Multiplication Approach

Let’s use the butterfly to help us. First, draw two loops as shown.

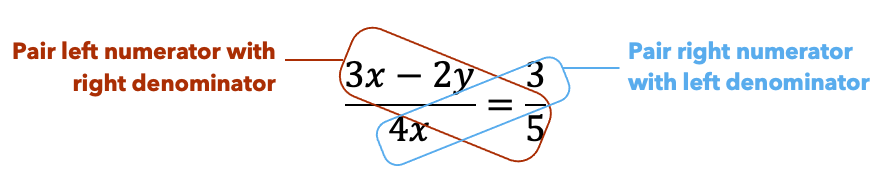
Next, we multiply the expressions in each loop. Use the distributive law to help you.

Then shift all the terms with  onto the LHS and the terms with  on the RHS.

Since we want the fraction , first, we make  alone on the LHS.

Then we divide by y throughout to get the desired  on the LHS.

Voila! The answer is .

What if the question instead asks for the ratio  ?

That’s right, we can write as  as  .

Let’s apply the cross-multiplication approach to the original question.

Question:

Given that  and  .

(a) Find the value of   .

(b) Hence, find the value of   .

Solving The Question Using The Cross Multiplication Method

Part (a):

Let’s use the butterfly to help us. First, draw two loops as shown.

Next, we multiply the numbers in each loop. Use the distributive law to help you.

Then shift all the terms  with onto the LHS and the terms with  on the RHS.

Since we want the fraction , first, we make  alone on the LHS.

Then we divide by  throughout to get the desired  on the LHS.

Part (b):

We now have to find the value of  . We already found the value of  in (a). Notice that we have not used .

The first question we must ask ourselves is…

How are ,  and  related?

Let me give you a hint. The product of two will give the other.

This is the missing link!

Now that we know how the 3 fractions are related, we can easily find !

Conclusion

After reading this blog post, I hope that you have gained a stronger understanding of when to use cross multiplication and how to apply the Butterfly Method when solving algebraic fractions.

Stay tuned for more articles that help you tackle challenging Math questions!