Introduction
Welcome back to another Secondary 1 Math blog post!
In this article, I will be giving you a step-by-step guide to answering a tricky Prime Numbers question involving a cuboid.
I noticed that students tend to lose points when answering this question because they missed an important keyword in the question.
Keep on reading if you want to find out what this keyword is and avoid making the same mistake!
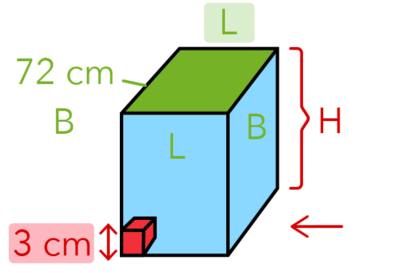
Let’s Take A Look At This Prime Numbers Question

Read Also:
We are going to solve this question using the Prime Factorisation Method.
But first, let us read the question together.
Step 1️⃣: Identify The Keywords
There are 140 pieces of 3 cm cubes.
In the very first sentence, there are actually two important pieces of information:
1️⃣ 140 pieces of cubes
2️⃣ 3 cm cubes
📦 What Does 3 CM Cubes Mean? 📦
It means that when you’re building the cube, each side of the cube is 3 cm.
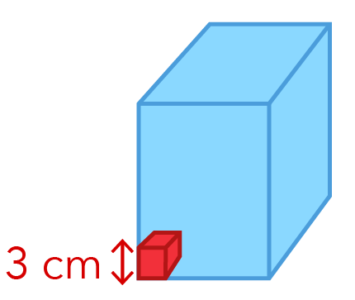
In this sense, the question is a bit tricky because we are not dealing with 1 cm cubes. We are now dealing with 3 cm cubes.
What about the 140 pieces? What does it mean?
Because we are going to make a cuboid, like the one in the diagram above, 140 pieces would make up the volume.
Step 2️⃣: Use The Prime Factorisation Method To Break Up The Volume
For the next step, we are going to break up 140 using the Prime Factorisation Method.
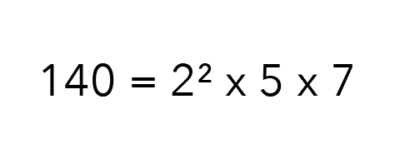
However, I like to break it up into individual factors so that I can see which numbers make up 140.
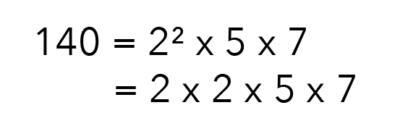
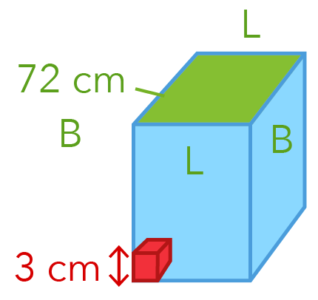
Step 3️⃣: Identify The Perimeter
Now, what’s the next clue?
The next clue is the perimeter of the base!

Some of you may be asking, “Where is the base?”
The base is actually at the top, which we highlighted in green below.
The perimeter is the 2 lengths (L) and 2 breadths (B) that we marked with green below.
Step 4️⃣: Find The Number Of Cubes Along The Perimeter
The 72 cm refers to the perimeter, but does it mean that there are 72 cubes along the lengths and the breadths?
The answer is no because we are dealing with 3 cm cubes. So there shouldn’t be 72 cubes.
Let us compute the number of cubes along the perimeter.

Step 5️⃣: Compute For The Number Of Cubes Along The Breadth & Length
Now, that we know that there are 24 cubes along the perimeter, we can narrow this down to:

How do we use the number 12 to help us find the two possible heights of the cuboid?
Where is the height of the cuboid? Let us first label it. We are going to use the letter H to label the height.
For labelling purposes, we’re going to follow these:

🤔 Why Do We Need NL & NB? 🤔
We cannot say that length + breadth = 12, because 12 is the number of cubes, not the actual perimeter.
So, it means that NL + NB = 12 cubes.
How is this information useful to us?
Because if we can guess the number of cubes along the length and breadth, which are the possible sums of 12, we can figure out our two possible heights.
Step 6️⃣: Guess & Check
Therefore, our next step is to start guessing. We’ll do that by drawing a table.
In the first column, let’s write down NL or the number of cubes along the length.
For the second column, let’s write down NB or the number of cubes along the breadth.
Finally, in the third column, let’s write down “Check,” which means that we’re going to use this column to either accept or reject the possible combinations of NL and NB.
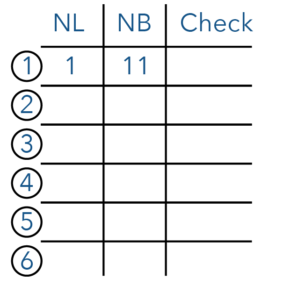
Remember that we have a total of 12. How do we get a sum of 12?
Can I begin with 0 and 12? Definitely not because I cannot have 0 cubes making up the length or the breadth!
So the smallest number will be 1. If one side is 1, we need the other side to have 11 cubes.
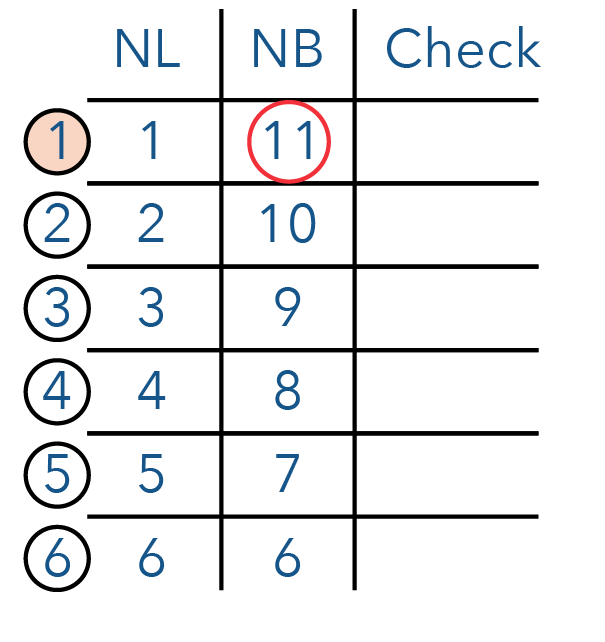
Let us first list down all the possible combinations.
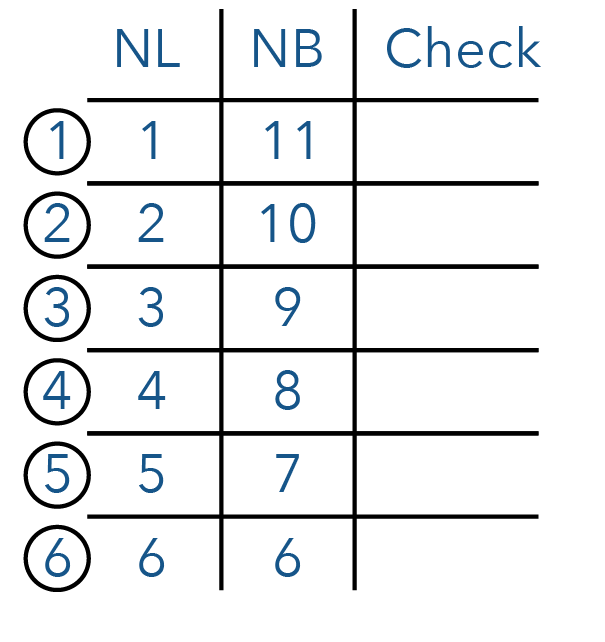
So there are 6 total possible combinations.
The question gave us a clue that there are only two possible heights, which means that out of the total of six combinations, we need to eliminate four of them.
Which ones do we eliminate? This is where we are going to use the prime factorisation of 140 that we solved earlier.
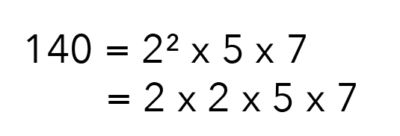
So if you look at the first combination, do you think it’s possible to have 11 cubes along the breadth?
Remember that 140 makes up the volume.
So 140 or 2 x 2 x 5 x 7 is actually the length x breadth x height.
If we are going to get 11 cubes along the breadth, I have to check my factors of 140. Do you think it’s possible to get 11 cubes? The answer is no.
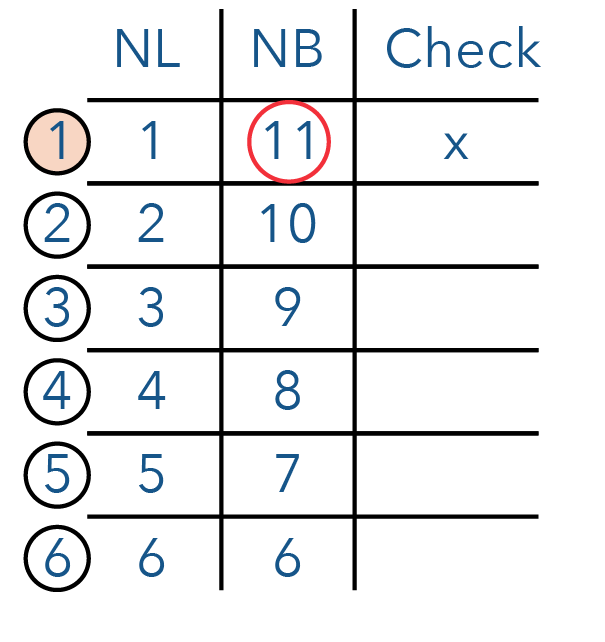
Now let’s take a look at combination 3.
Is it possible to get 3 cubes along the length? Again, if you look at the factors of 140, the answer is no, because we cannot find 3 anywhere in the factors of 140.
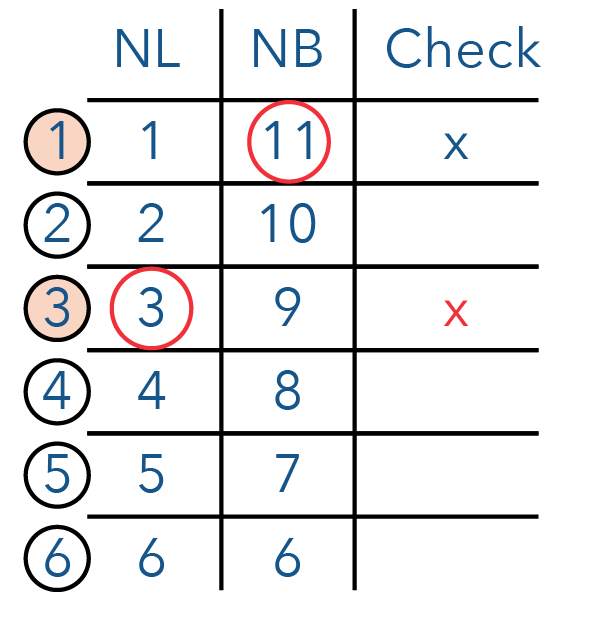
Now, let us look at combination 6.
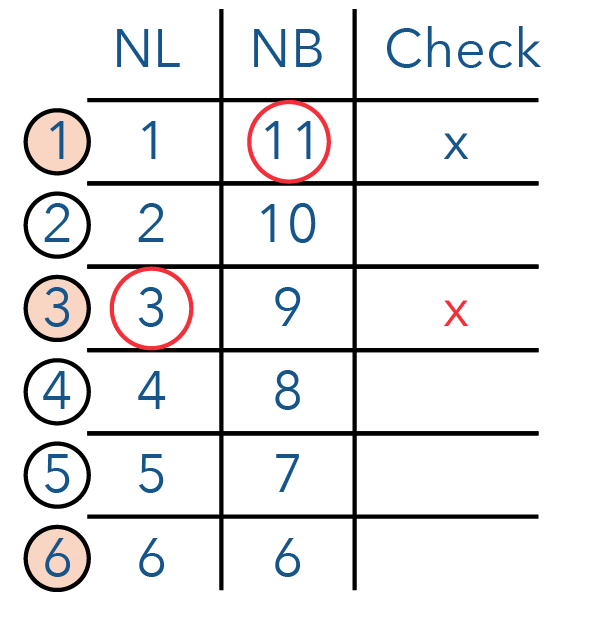
How do we get 6? 6 is actually 2 x 3. And because we cannot have a 3 in our factors of 140, this is also not a possible answer!
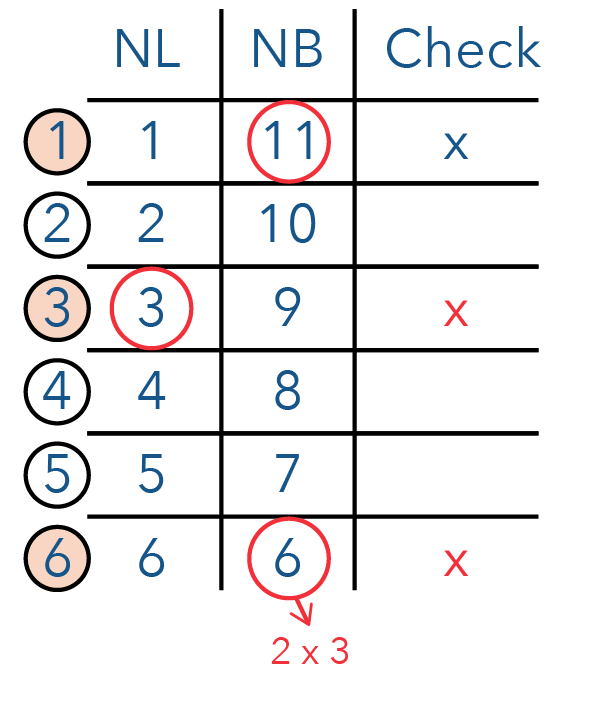
This leaves us with 3 possible combinations — numbers 2, 4, and 5. However, we only need 2 possible heights so we have to eliminate one of them.
Let us look at combination 4!
We can make up 4 from our factors of 140 because there is 2 x 2, which gives us 4.
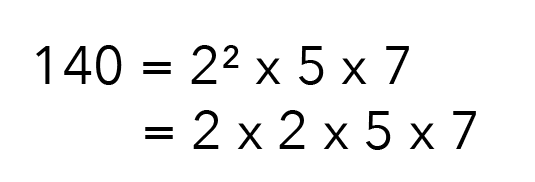
But 8 is actually 2 x 2 x 2. I need three sets of 2s to make up 8, which is impossible because we are only left with 5 and 7. We no longer have an extra 2.
So combination number 4 is also out of the question!
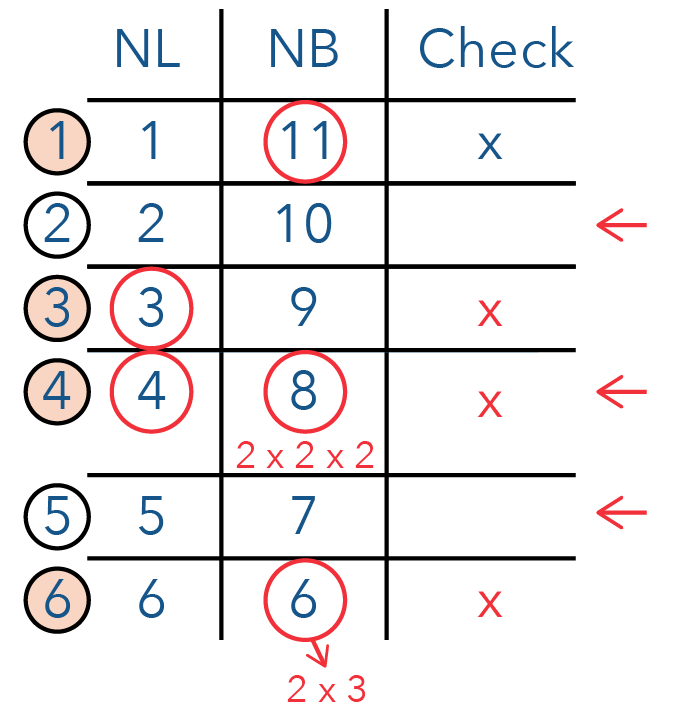
This is good news because we are only left with 2 combinations — 2 and 5.
So let’s check combination 2 first!
Can the number of cubes along the breadth be 10? Yes, because I have 2 and 5, which are factors of 140. For the number of cubes along the length, we have 2, which is also a factor of 140.
So this is possible!
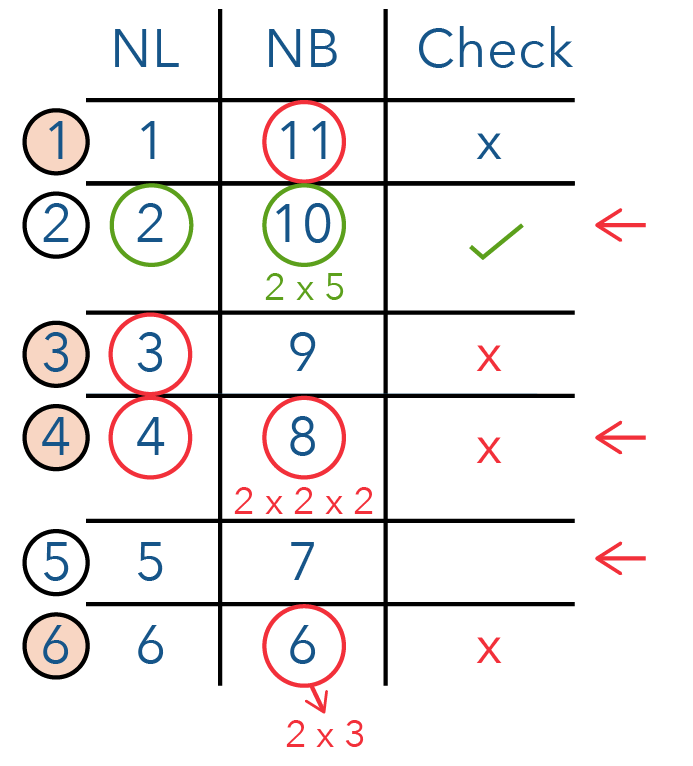
What about 5 and 7 for combination 5?
The numbers 5 and 7 are also factors of 140. So this is another possible combination!
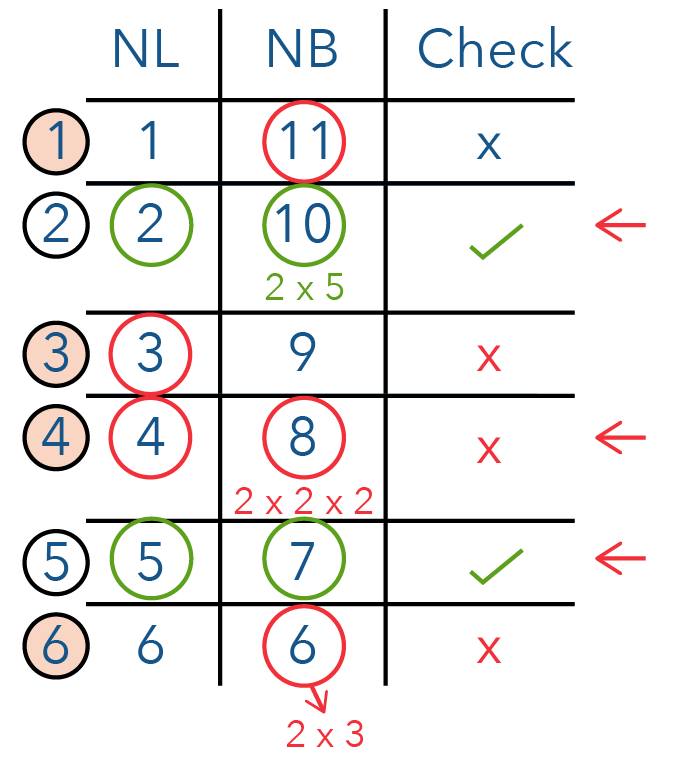
Step 7️⃣: Find The Possible Heights
We can finally answer the question! How are we going to do that?
Recall that we are dealing with 3 cm cubes. So, the first step is to find the two possible heights.
So I’m going to label the first height as H1, which means that if I have 140 cubes, in order to find the height, this would be the volume divided by the base area.
So if I take 140 divided by base area which are 2 and 10, I will get 7.
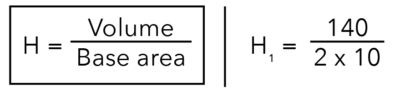
But recall that it’s not the actual height because we are not dealing with 1 cm cubes. We are dealing with 3 cm cubes.
So it will be 7 x 3, which is 21 cm. So the first possible answer is 21.
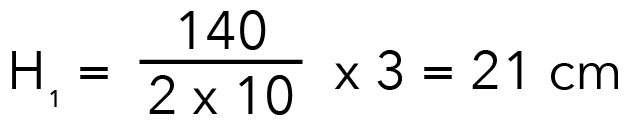
The second possible answer would be the volume, 140 divided by base area (combination 5), which is 5 x 7. This will give us 4 cubes.
But again, each cube is 3 cm in length, so we will multiply it by 3. Therefore, our answer will be 12 cm.
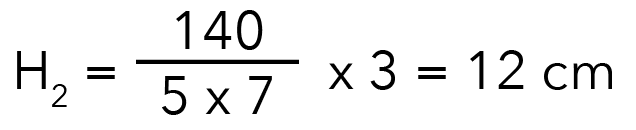
Suggested Answer
H1 = 21 cm
H2 = 12 cm
Conclusion
I hope that after reading this S1 Math blog post, you have learned the importance of reading the question carefully and taking note of the keywords.
Some might assume that the perimeter of the base is made up of 72 cubes. But the question states that the cuboid is made up of 3 cm cubes so the perimeter of the base cannot be made up of 72 cubes.
Remember to follow the 7 steps that we did to solve similar questions in future!
Step 1️⃣: Identify The Keywords
Step 2️⃣: Use The Prime Factorisation Method To Break Up The Volume
Step 3️⃣: Identify The Perimeter
Step 4️⃣: Find The Number Of Cubes Along The Perimeter
Step 5️⃣: Compute For The Number Of Cubes Along The Breadth & Length
Step 6️⃣: Guess & Check
Step 7️⃣: Find The Possible Heights
See you in the next S1 Math blog post!

If you like our methodology, we've some ongoing weekly Math classes:







