2018 Catholic High School (CHSP) P5 Math Examination Paper Analysis

Introduction

Welcome back to another P5 Math word problem sums blog post!

We previously discussed how to use the Model Drawing Technique. Click this link if you missed that!

In this article, we will be analysing a question on the topic of Whole Numbers from the 2018 Catholic High School (CHSP) P5 SA1 Examination Paper.

You can also watch my explainer video for free by visiting The Pique Lab’s YouTube channel!

Let Us Take A Look At This Whole Numbers Question

Source: Catholic High School — 2018 P5 SA1 Examination Paper [Q10]

Finding The Keywords

Let us read the question.

Mrs Chan bought some pencils for a group of pupils.

Do we know the exact number of pencils she bought? We do not know because the question only states “some.”

Let us draw a model to help us remember that Mrs Chan bought “some” pencils.

Next, do we know how many pupils are in the group?

The question did not state as well, which may indicate that this is what we need to solve.

Let us use 1 unit as the unknown number of pupils.

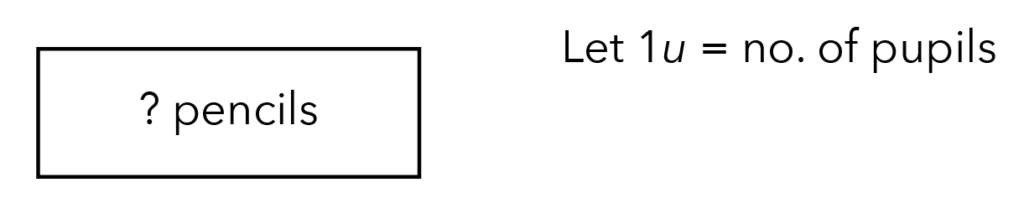
Let us continue reading the question.

If she gave each pupil 3 pencils, she would have 13 pencils left.

If she gave each pupil 5 pencils, she would need 5 more pencils.

In these two sentences, we see the word “If.”

We shall refer to our first “If” sentence as our Case 1.

In Case 1, we saw the keyword “left”.

Does this mean that Mrs Chan has too many pencils or too few pencils?

The sentence says that she would have 13 pencils left. This means that she bought too many pencils and has excess.

Let us refer to the second “If” sentence in the question as our Case 2.

For Case 2, the keyword that we read is “need”.

Does it mean that Mrs Chan has too many pencils or too few pencils?

The sentence says that Mrs Chan would need 5 more pencils, which means that she has too few pencils and she does not have enough. In this case, she has a shortage.

This question is an example of where we can apply the Gap & Difference Method, also known as Excess and Shortage.

Using The Gap & Difference Method

💡 When Can We Use the Gap & Difference Method?💡

1️⃣ When you see the keyword “If” in the question twice. (We can see the two “Ifs” underlined above)
2️⃣ When you see two cases or scenarios. (We have indicated them as Case 1 and Case 2 in this question).
3️⃣ When there is a situation of excess and excess or shortage and shortage or excess and shortage. (There is an excess and a shortage in this question).

Now, let’s start drawing our models to solve the question.

Let’s recap: Mrs Chan has some pencils as indicated by the Black Model that we drew earlier.

Let us now draw Case 1, which we will call our Blue Model.

First, write down what Mrs Chan has — according to Case 1, she gave away 3 pencils to each pupil.

Next, we can see the keyword “left,” which means there is an excess of 13 pencils.

Let us cut a portion from our model to show this excess.

Keep in mind that we have 1 unit of pupils and Mrs Chan actually gave away 3 units of pencils.

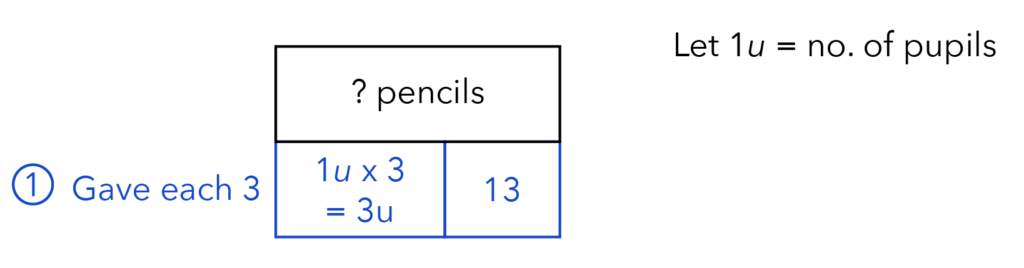
Let us now move on to Case 2, which we will refer to as our Green Model.

Like what we did in our Blue Model, let us write down what Mrs Chan has.

Next, the keyword “need” was used in Case 2, which means that she does not have enough pencils.

Let us help Mrs Chan have enough pencils for all her students by adding 5 extra pencils using dotted lines. Take note that Mrs Chan does not actually have these 5 pencils.

With all these pencils and keeping in mind that we have 1 unit of pupils, Mrs Chan actually gave away 5 units of pencils in Case 2.

It is important to note that if you can make the parts equal for your model, always do it because this will help you solve the question.

Let us also add the 3u and 13 from our Blue Model.

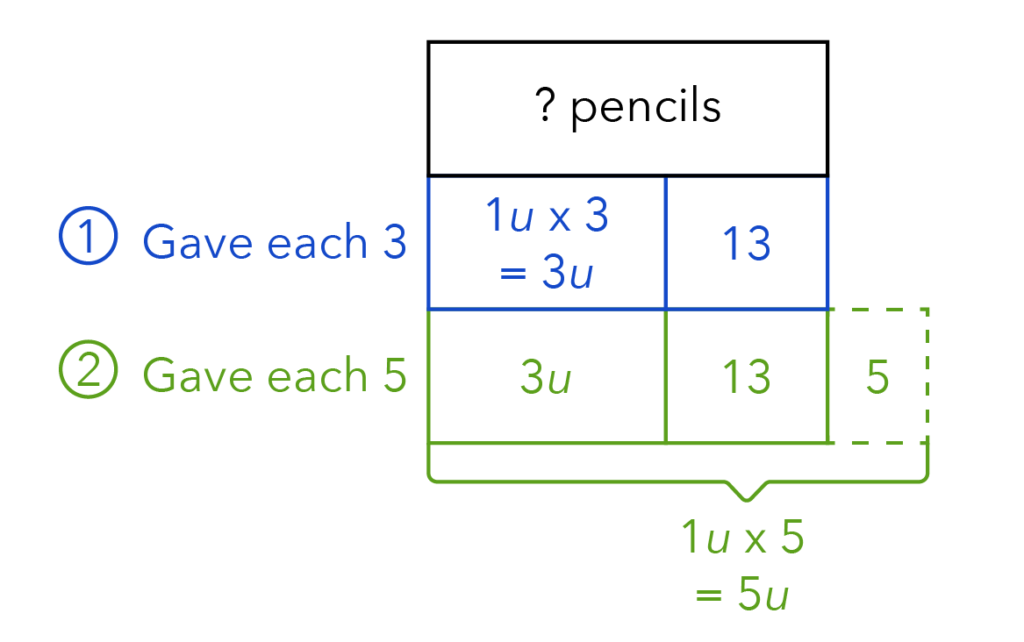
What else can we add to the model to solve the question?

There is a clear gap in the units, and in this case, it is 5 units – 3 units, which will give us 2 units.

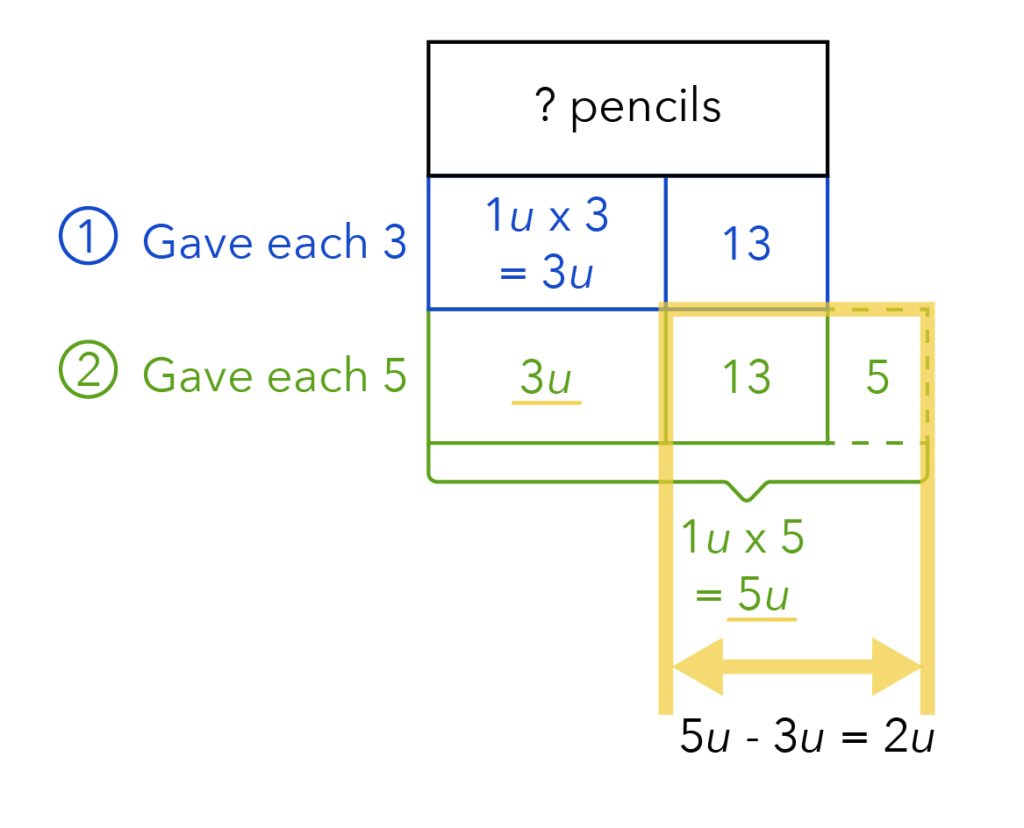
What are these 2 units?

Let’s look at the model again.

The act of Mrs Chan giving 3 pencils in Case 1 and 5 pencils in Case 2 to each pupil gives us a difference of 2 pencils per pupil.

With all the differences added up, a gap of 2 units is produced. This gap of 2 units is shown on the model as 13 + 5, which gives us 18 units.

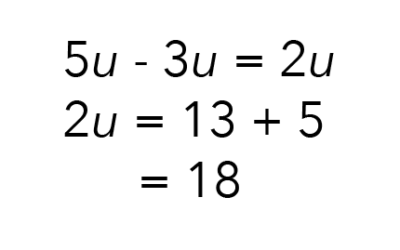
Let us now solve for 1u.

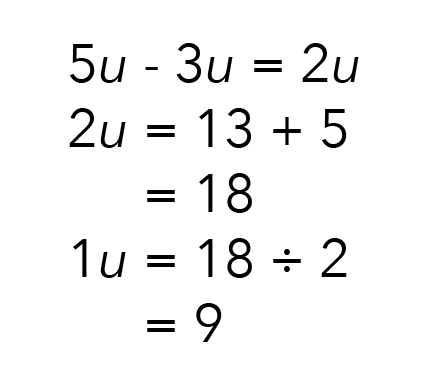
Now that we know the value of 1 unit, let us go back to our question.

Source: Catholic High School — 2018 P5 SA1 Examination Paper [Q10]

The question wants us to find out how many pupils were in the group.

Remember that earlier, we assigned 1 unit to be the unknown number of pupils.

Since we have derived that 1 unit is 9, the answer to this question is 9 pupils.

Answer For Q10

9 pupils

Conclusion

After reading this P5 Math blog post, I hope that you learnt how to use the Gap & Difference Method when solving P5 Math Whole Numbers questions.

To help you remember when to use this P5 Math problem-solving technique, remember these 3 identifiers:

1️⃣ When you see the keyword “If” in the question twice.
2️⃣ When you see two cases or scenarios.
3️⃣ When there is a situation of excess and excess or shortage and shortage or excess and shortage.

Remember to follow our blog for more P5 Math blog posts!