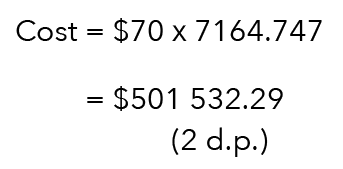Trigonometry: How To Solve Bearings Word Problems

Introduction

Welcome to a new blog post on Trigonometry!

In this article, we will be analysing a question on the topic of Trigonometry from the 2020 Punggol Secondary School (PGSS) S3E SA2 Examination Paper.

Read this blog post if you want to solve Math questions involving Bearings better and faster.

Alternatively, you can also watch my explainer video for free by visiting The Pique Lab’s YouTube channel!

 

Let’s Take A Look At This Trigonometry Question

Source: Punggol Secondary School — 2020 S3E SA2 Examination Paper [Q7]

In this question, we are given a diagram, ABC, which represents a horizontal triangular field and a vertical flagpole, AP.

We are told that B is 85 metres from A on a bearing of 025° and that point C is 170 metres away from point A.

We are also given length BC as 180 metres and the height of the flagpole is 12 metres.

Let us start by establishing what a bearing is.

🔁 What Is A Bearing? 🔁

A bearing is the angle in degrees which is measured clockwise from the north direction. It is usually stated as a three-digit system.

Let’s say we have two points, A and B, and they are separated by a certain distance apart.

If we are interested in finding out the bearing of A from B, we must first identify the starting point.

🏁 How To Identify The Starting Point 🏁

Remember that the starting point is always after the word from.

In (a)(i), B is our start point and A is our endpoint.

Source: Punggol Secondary School — 2020 S3E SA2 Examination Paper [Q7]

We shall now go to the start point and draw a north direction, which is typically drawn in the vertical direction as shown in the diagram below.

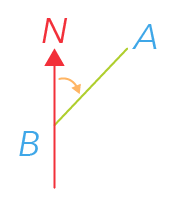
Remember that we want to find the bearing of A from B so we will draw a clockwise angle starting from the north direction and stop when it touches the green-coloured line.

Let’s say that this angle is 10°. We’ll say that the bearing of A from B is 010°.

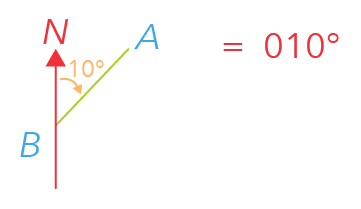
This is what it means by a three-digit system.

Now that we know what a bearing is, let us proceed to solve the question.

Let’s Analyse Part (A)(I)

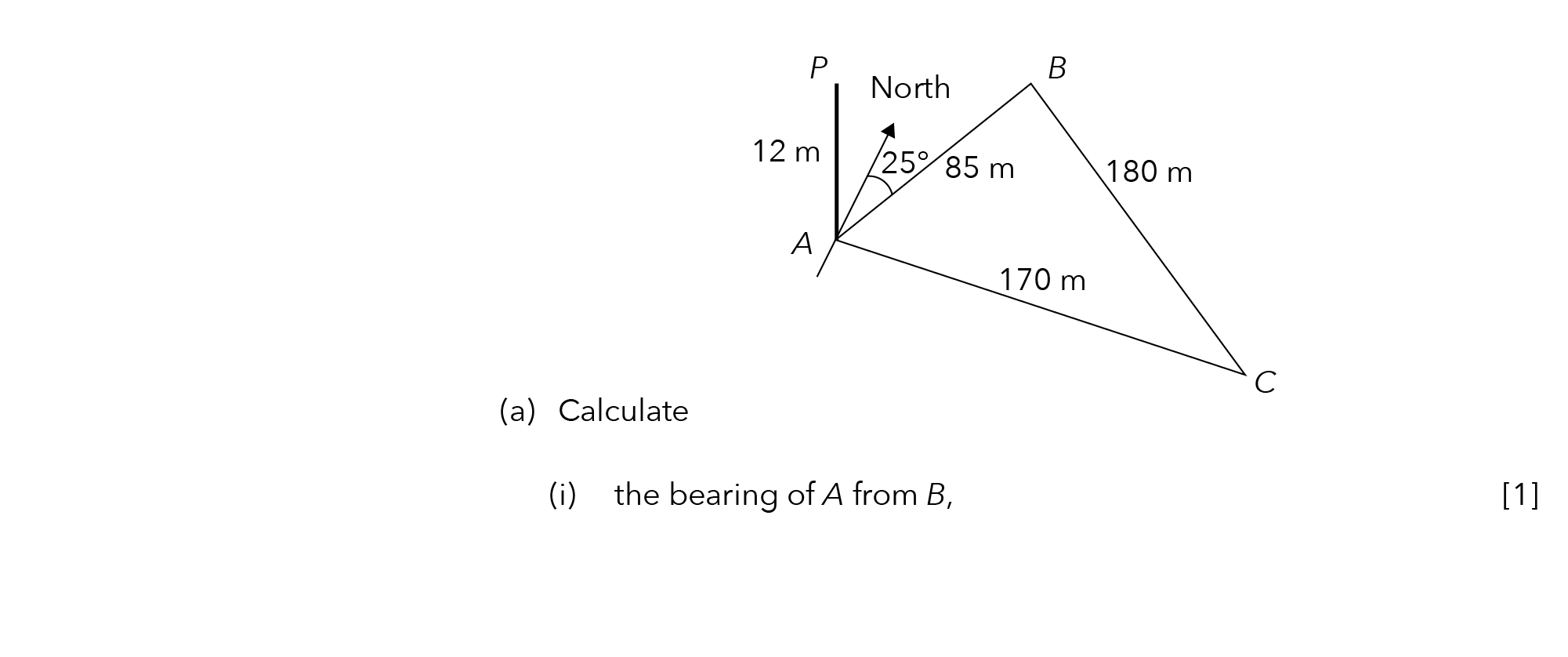
Source: Punggol Secondary School — 2020 S3E SA2 Examination Paper [Q7]

Since we are interested in finding the bearing of A from B, we must first find the start and end points.

Recall that the start point is always after the word from. In (a)(i), A is our endpoint, while B is our starting point.

In our diagram, we shall now proceed to point B and draw in the north direction.

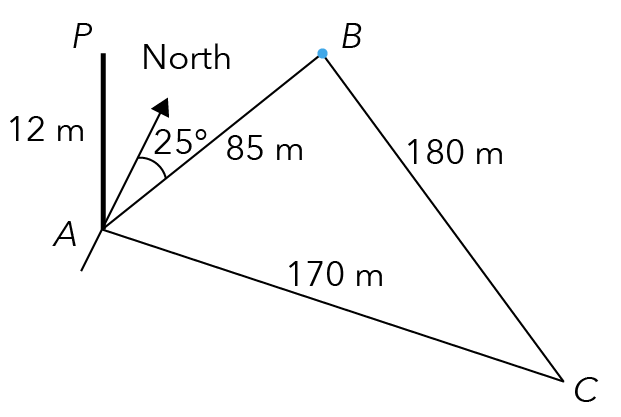
Source: Punggol Secondary School — 2020 S3E SA2 Examination Paper [Q7]

What do you notice in the north direction in our diagram?

The north is not pointing vertically upwards but rather is in a slanted direction.

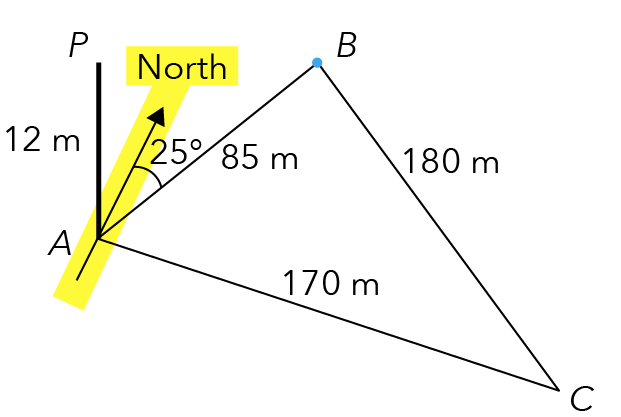
Source: Punggol Secondary School — 2020 S3E SA2 Examination Paper [Q7]

Remember to be mindful of that and draw in the north also a bit slanted.

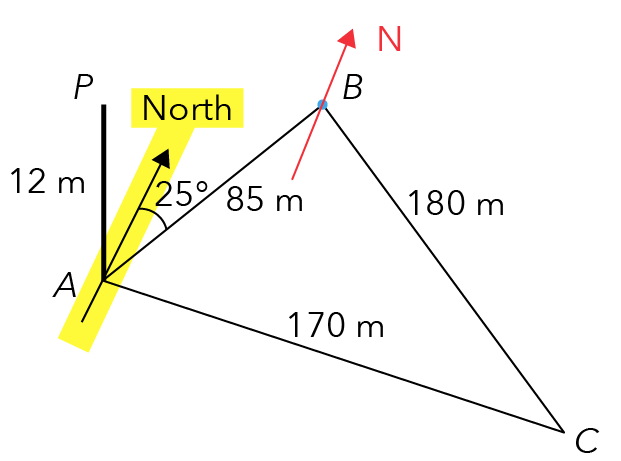Source: Punggol Secondary School — 2020 S3E SA2 Examination Paper [Q7]

So how do we calculate the bearing of A from B? Let us draw in the angle. It will be moving clockwise from the north, all the way until it touches the line connecting A and B.

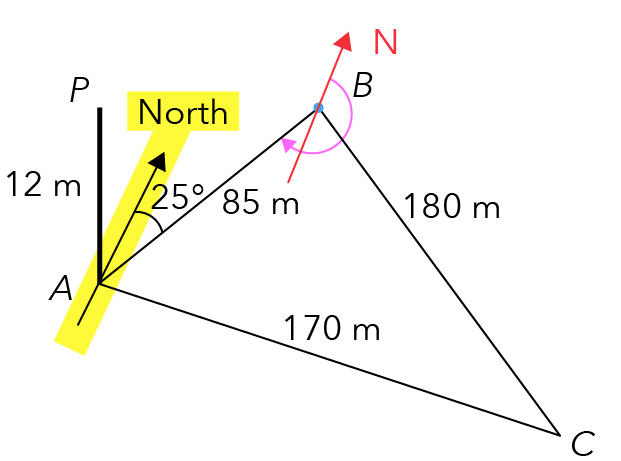
Source: Punggol Secondary School — 2020 S3E SA2 Examination Paper [Q7]

We are interested in finding the pink-coloured angle, but we will have to make use of the green-coloured angle below first.

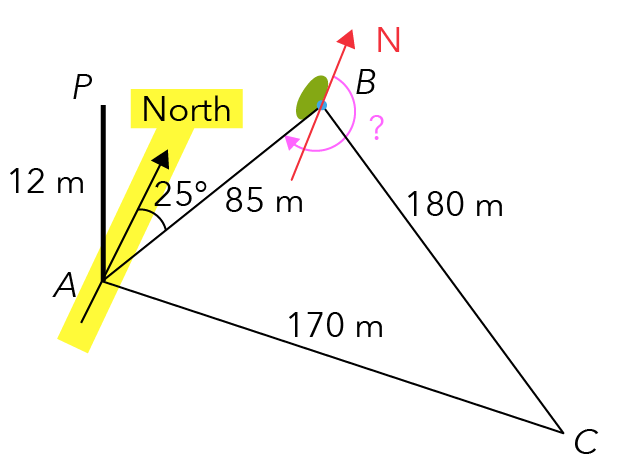
Source: Punggol Secondary School — 2020 S3E SA2 Examination Paper [Q7]

Notice that in our diagram, there are a total of two north directions drawn for us.

Because they are pointing in the same direction, we can conclude that these two are parallel to one another.

What deduction can we make about the 25° we highlighted in blue and the green-coloured angle?

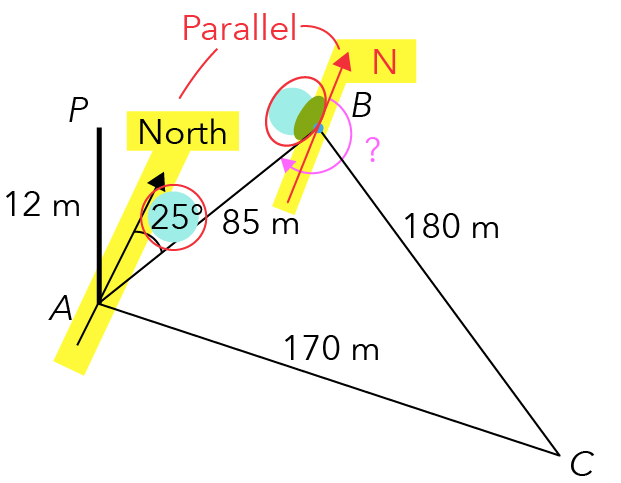
Source: Punggol Secondary School — 2020 S3E SA2 Examination Paper [Q7]

Since they are created by two parallel lines, they are a pair of interior angles.

🍰 What Are Interior Angles? 🍰

They are two angles that sum up to 180° and are formed in between parallel lines.

So how do we calculate the green-coloured angle?

We will take 180° and subtract 25° to get 155°.

 

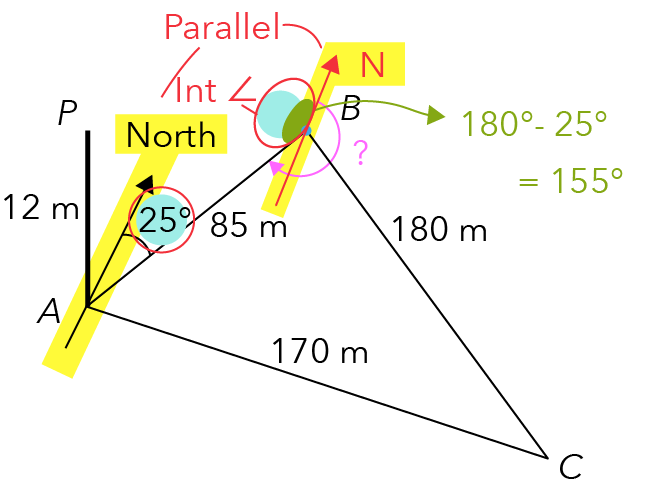
Source: Punggol Secondary School — 2020 S3E SA2 Examination Paper [Q7]

We can now proceed to solve part (a)(i) by taking one full revolution, which gives us 360° around point B. Then, subtract the green-coloured angle of 155° to get the final answer of 205° as the bearing of A from B.

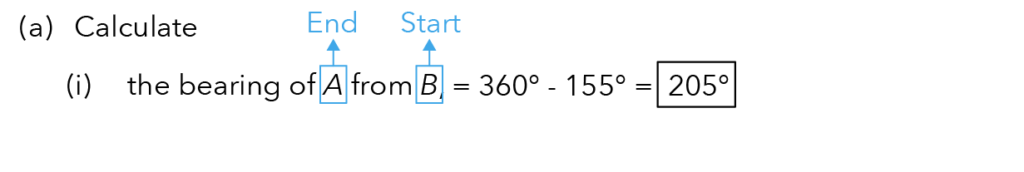
Source: Punggol Secondary School — 2020 S3E SA2 Examination Paper [Q7]

Answer For Part (A)(I)

205°

Let’s Analyse Part (A)(II)

Source: Punggol Secondary School — 2020 S3E SA2 Examination Paper [Q7]

In part (a)(ii), we are required to find ∠ABC.

Let us start by drawing a simple sketch of the triangular plane ABC.

∠ABC is annotated by the green-coloured angle. How are we going to find its value?

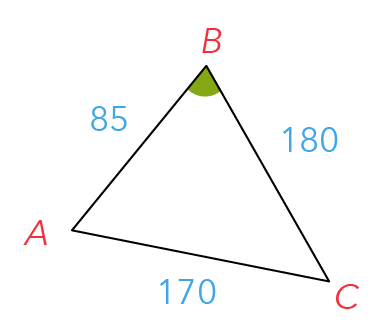
Notice that we are given all three sides of the triangle, but we do not have any interior angles.

Hence, we will be using the Cosine Rule for this question.

💡 What Is The Cosine Rule? 💡

Cosine Rule helps us find unknown lengths and angles along a non-right angle triangle.

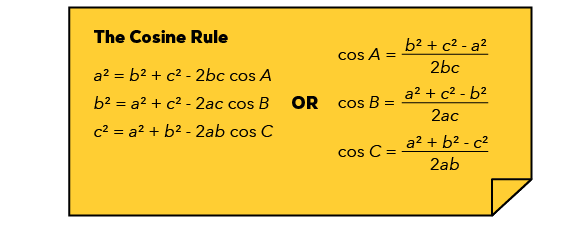
In this case, because we are interested in finding an unknown angle in a non-right angle triangle, we’ll use the variation on the right.

Let us substitute the values into the formula.

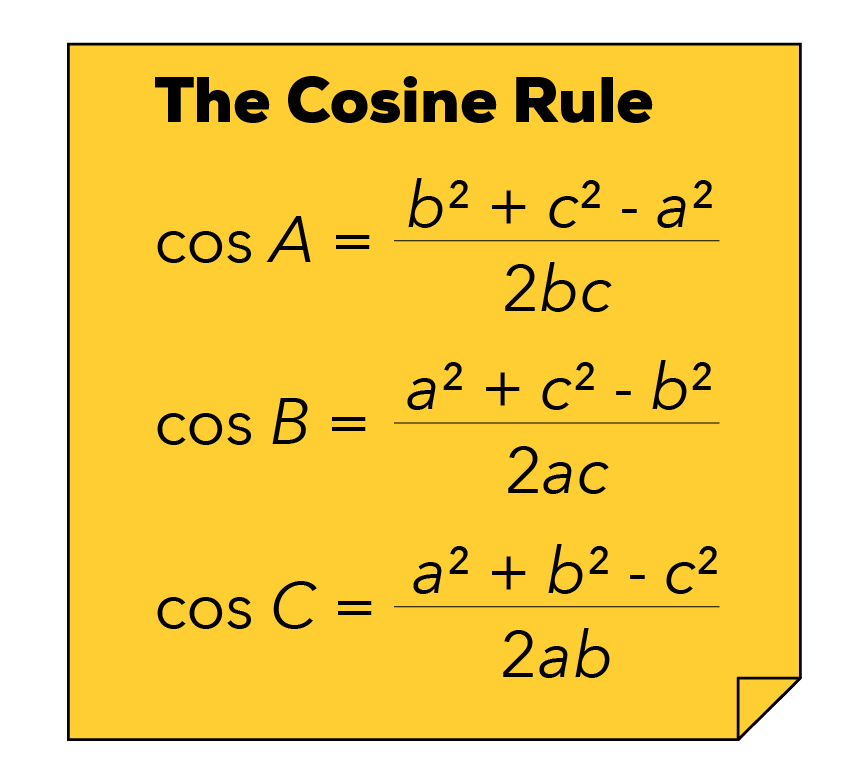
When we use the Cosine Rule, it is important to note the corresponding angles and the value we subtract in the numerator.

How do we identify this pairing here?

Because we’re interested in ∠ABC, if we reference our diagram on the left, take note that the A value we subtract encircled in blue will always be the side directly opposite the angle.

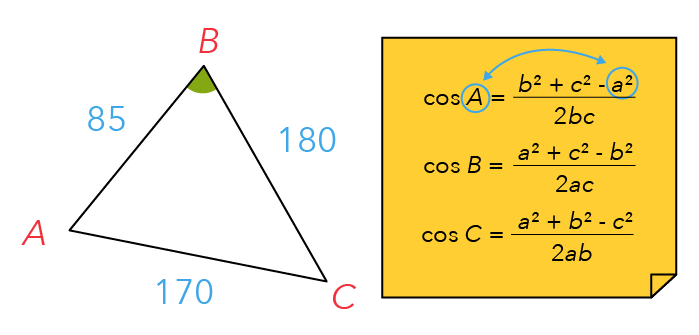
So in this case, the value of a is 170, b is 85, and c is 180.

Let us set up the Cosine Rule now.

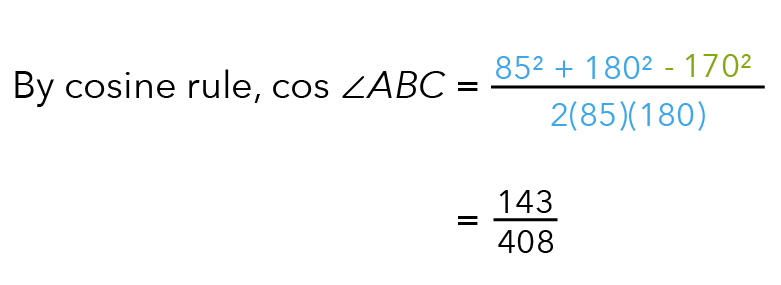
To find angle ABC we shall take a cosine inverse of 143/408.

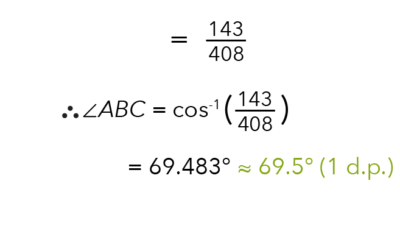
Answer For Part (A)(II)

69.5°

Let’s Analyse Part (B)

Source: Punggol Secondary School — 2020 S3E SA2 Examination Paper [Q7]

In part (b), we are given a rate relating the cost of the plot of land to its area in square metres.

We want to calculate the cost of the land occupied by the triangular field ABC.

Let us start by finding the area of this plot of land.

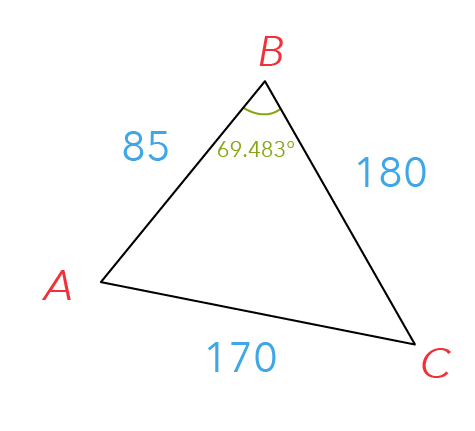
How do we go about it?

The area of a triangle can be calculated using the formula 1/2 x base x height.

But are we going to use this to answer this question? It is not wrong to use it, but it will be very tedious as it involves multiple steps.

To help you save time, we’ll use this formula:

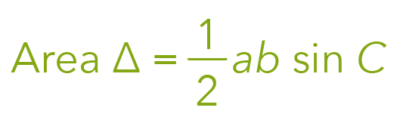
A and B here represent two sides of the triangle, while C is what we call the included angle that is required to calculate the area itself.

What does it mean to be an included angle?

If we refer to the triangle below, we see that we have one angle given to us, which is 69.483° calculated from part (a)(ii).

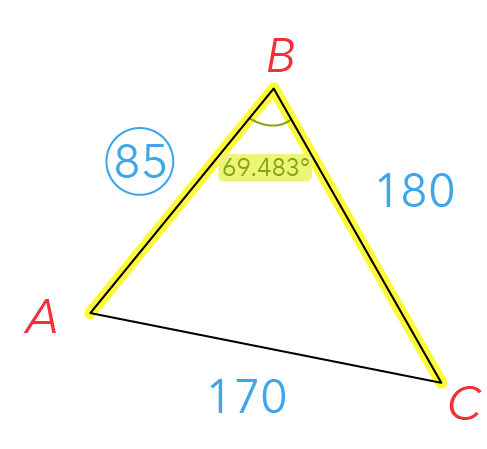
This angle is created by two sides of the triangle — AB and BC, with the values of 85 and 180, respectively.

So together, these two sides here create the ∠ABC, which is what we call the included angle.

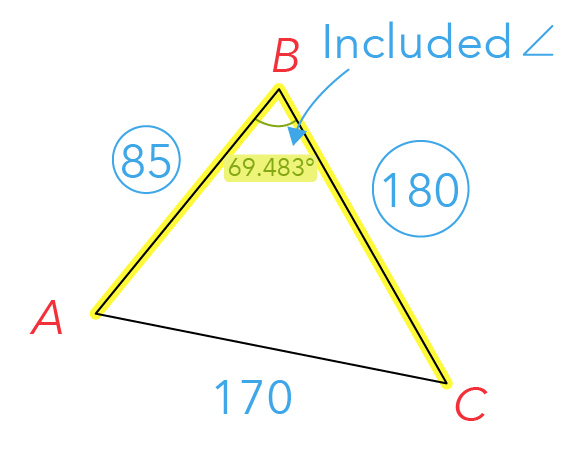
Let us now substitute the values into the area formula.

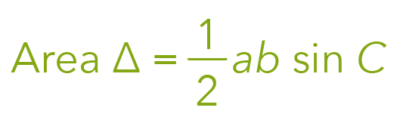
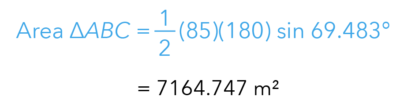
Therefore, the area is 7164.747 square metres.

To solve for the cost, we will multiply the area by the rate given in the question, which is $70.

Answer For Part (B)

$501 532.29 (2 d.p.)

Let’s Analyse Part (C)

Source: Punggol Secondary School — 2020 S3E SA2 Examination Paper [Q7]

In part (c), we are given a man who is walking along BC as shown in the diagram below.

Also, recall that in the question, there was a flagpole at point A denoted by AP, with a length of 12 metres.

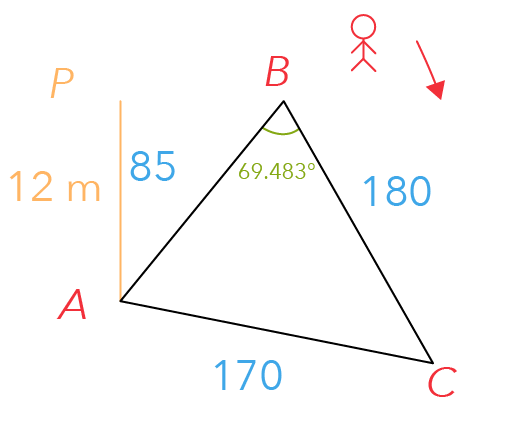
In part (c), we are interested in calculating the greatest angle of elevation of the top of the flagpole when viewed by the man as he travels from point B to point C.

Let us begin solving this by finding where exactly along BC will we get the greatest angle of elevation.

It is the shortest distance from the base of the flag pole, which is denoted by point A in the diagram.

Where exactly is that point?

It will be the perpendicular distance from point A, all the way to line BC.

Let us label this as point M. It is at this point where the greatest angle of elevation will be obtained.

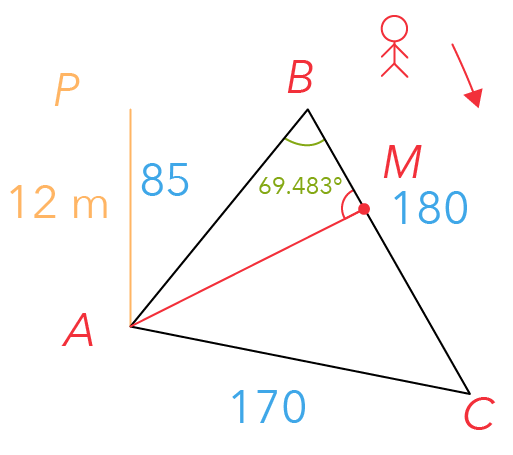
If we connect points P and M in a straight line, we’ll obtain a triangle as highlighted in yellow.

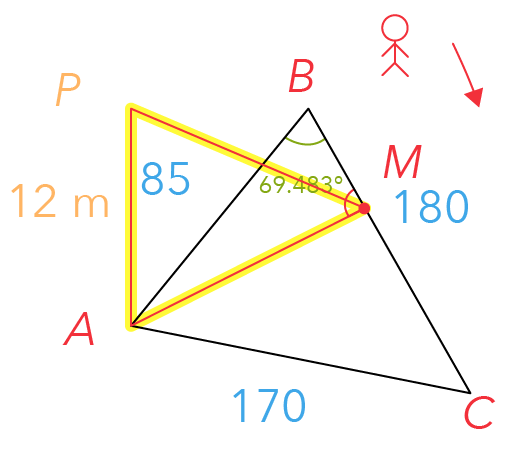
Let us sketch out triangle PAM.

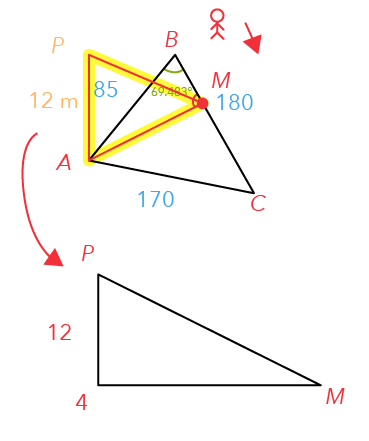
Since the vertical flag pole is placed on horizontal ground, we note that the angle PAM is a 90-degree angle.

Where is the greatest angle of elevation in this triangle?

It will be at ∠AMP.

How do we find this value?

We can make use of the trigonometry concepts that we learned before to evaluate this value.

When given an unknown angle in a right-angled triangle, we need a minimum of two sides.

At this point, we have one side — AP. However, we do not have sides PM and AM.

To solve for the angle required, we need to find either PM or AM. Which side should find?

For this question, we are going to look for side AM because we have enough information to solve for this value.

Let us review the diagram.

What can we infer about AM with respect to triangle ABC?

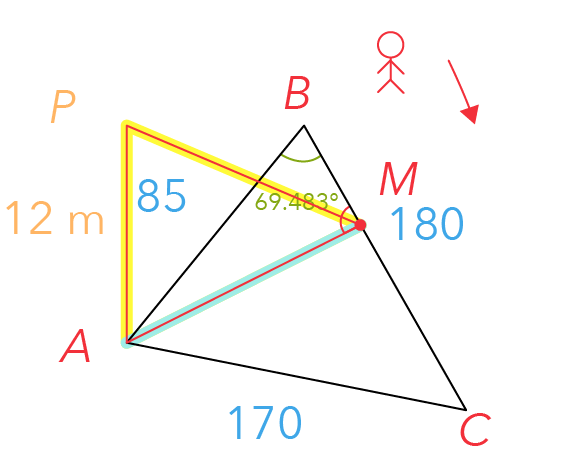
It is actually the perpendicular height of the triangle itself.

Recall from part (b) that we found the area of triangle ABC which was 7164.747.

Since we have the perpendicular height identified, we can make use of our 1/2 x b x h formula.

We know that height was given as side AM. So what should we choose as the base? It will be side BC.

Let us now substitute the values to find AM.

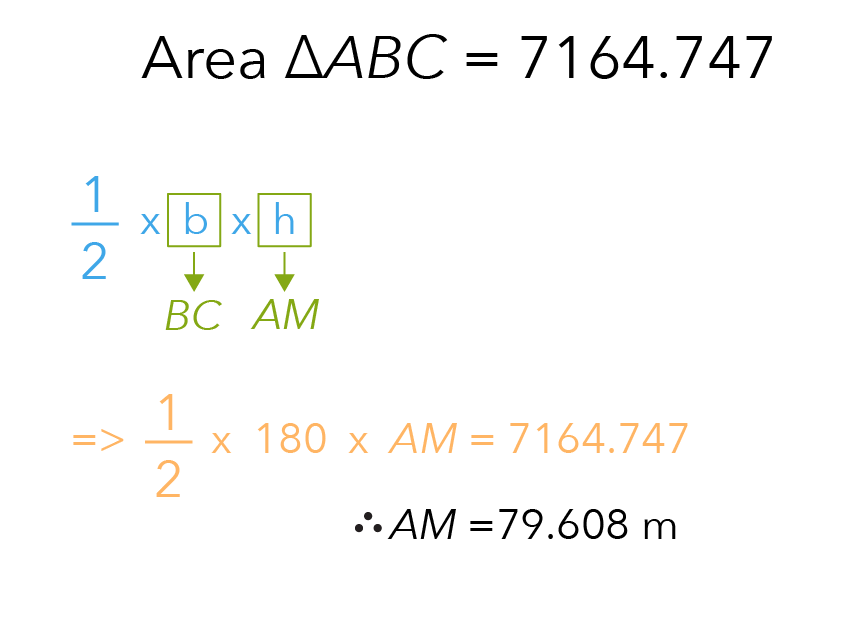
Going back to our triangle PAM, we can now label AM as 79.608.

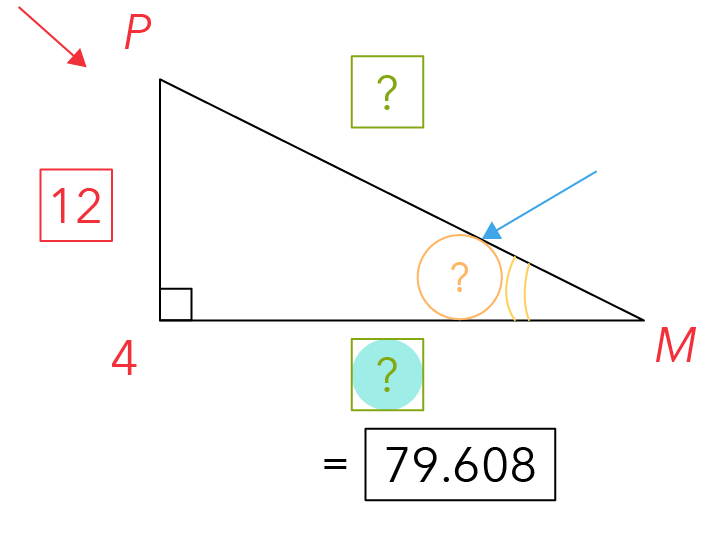
With two sides of the triangle, we can now use trigonometry to solve for the angle required.

AP plays the role of our opposite side, while AM plays the role of our adjacent side.

What trigonometry function should we use to solve for the angle required?

We will use the Tangent Function to obtain the greatest angle of elevation:

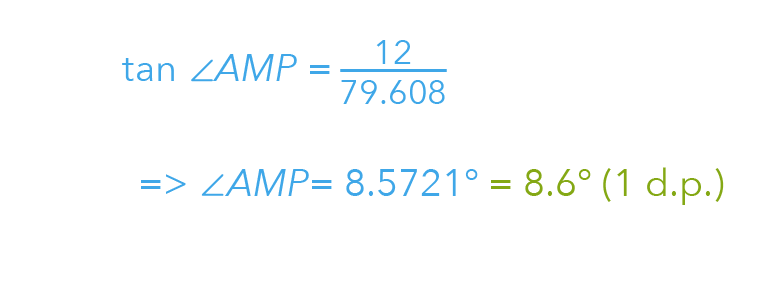
Answer For Part (C)

8.6°

Conclusion

I hope that after reading this S3 A-Math blog post, you have learned the following:

• How to solve word problems involving bearings.
• How to use the Cosine Rule to find unknown lengths and angles along a non-right angle triangle.
• How to find the area of a triangle when sides a, b, and included angle are available.
• How to use the Tangent Function to obtain the greatest angle of elevation.

Keep following our blog for more S3 A-Math exam tips on Trigonometry!