Introduction
How do you simplify a Secondary 3 A-Math exponential expression like the one below, without using a calculator?
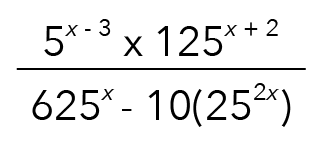
Some of you might feel overwhelmed by the terms. But don’t worry because I will teach you a step-by-step guide to solving such complex-looking Exponentials questions.
You can also watch my explainer video for free by visiting our YouTube channel.
Let’s Take A Look At This Exponentials Question

Source: St. Gabriel’s Secondary School – 2020 S3 A-Math SA2 Examination Paper [Q4]
Read Also:
Step 1️⃣ Study the terms involved in the expression
Let us begin by studying the terms involved in this expression.
In the term highlighted in yellow below, we notice a base term of 5.
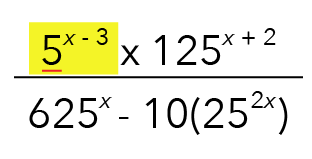
Can this term be rewritten to a simpler base?
No, it can’t.
What about the remaining terms we highlighted in green, blue and orange below? Can they be rewritten to a simpler base?
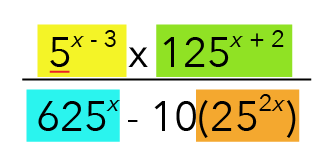
To answer that, we will consider the first few powers of 5:
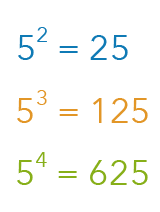
What do you notice about the first few powers of 5 and the given terms in our expression? The terms can be rewritten to a common base of 5, which leads us to our next step.
Step 2️⃣ Rewrite terms to their common bases
Now, let’s try it out.
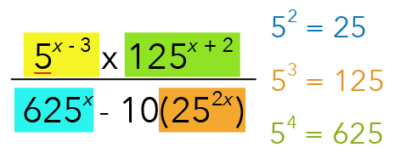
We can rewrite the term highlighted in green as![]() .
.
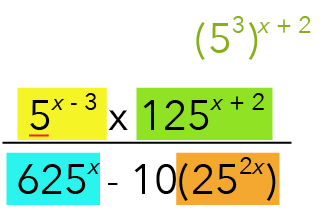
Let us now move on to the term highlighted in blue.
We will have ![]() .
.
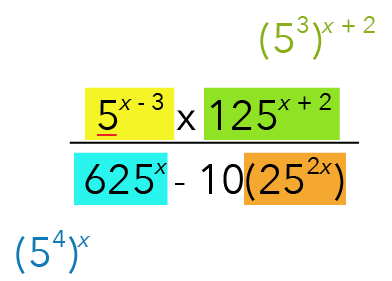
What about the term highlighted in orange?
We will get ![]() .
.
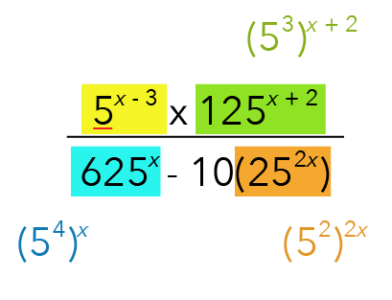
Now that we have rewritten the terms to their common bases, notice that the green, blue, and orange stripes all contain brackets, which I highlighted in yellow.
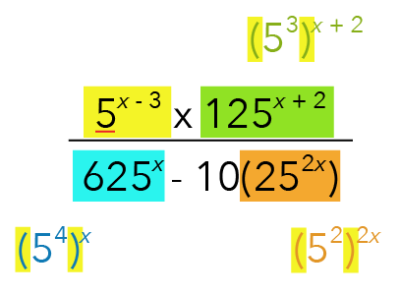
We can remove these brackets by proceeding with our next step.
Step 3️⃣ Activate the Laws of Indices
I have discussed the Laws of Indices in detail in a previous blog post. Click this link if you want a quick recap of the Laws of Indices.
The Law of Indices that we will be using here is as follows:
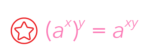
Recall that this law tells us that when we have a base term that has been raised to two powers, first by x and then by y, we will simplify by multiplying the powers together.
Let us try this law in our expression.
For the green stripe, when we multiply the powers together, please be careful here and remember that we will distribute the 3 to x and 2.
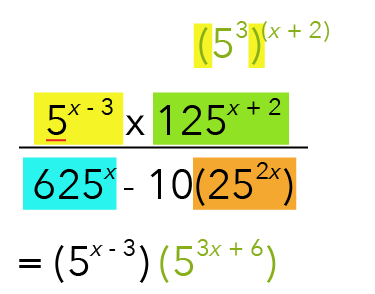
Let us move on to the denominator.
For the blue stripe, we will get ![]() .
.
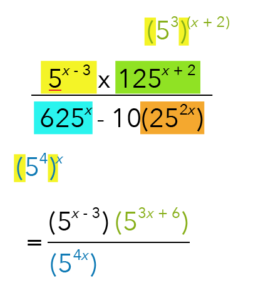
What about the orange stripe?
We will get ![]() .
.
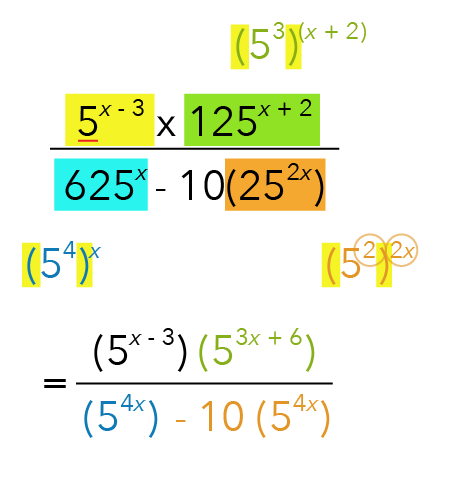
Now let us continue by studying our numerator and denominator separately. In the numerator, we see that there is a product of two terms and they share a common base of 5.
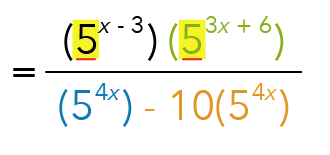
For expressions in such format, we can simplify them using the following law of indices:

Recall that in this law, when we take the product of two terms that share the same base, we simplify them by adding up their powers together.
So for the numerator term, we can simplify it by adding up the powers together to get: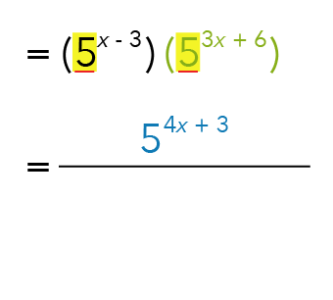
Next, let us look at the denominator:

Do you see a common factor? It is ![]() .
.
Hence, we can factorise it out and introduce a bracket.
What is left in the bracket? It will be 1-10.
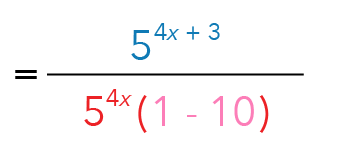
At this point, do you notice that the numerator and the denominator contain a common-looking term?
That term is 54x.
This means that we can simplify further by cancelling the common term highlighted below.
But how do we do it?
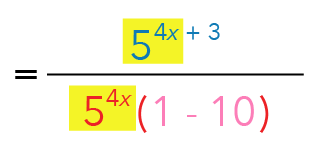
Let us look back at our law of indices and move from right to left.
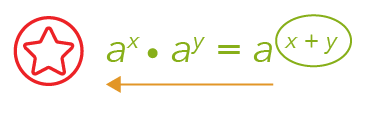
The idea here is to perform a split of the expression into two different parts.
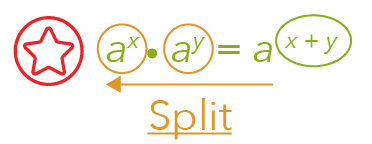
Let us look at the numerator. If we split the term according to the law above, we will obtain:
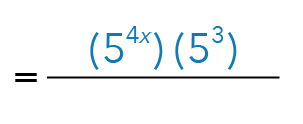
In the denominator, we will be left with:
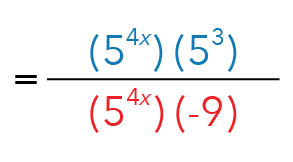
We can now cancel the common factor and obtain our final answer. Since we know that 53 is 125, our final answer will be -125/9.
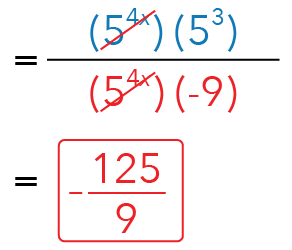
Suggested Answer

Conclusion
I hope this Exponentials blog post has helped you feel more confident in tackling Exponentials questions, even without using a calculator.
To simplify exponentials quickly and accurately, make sure to follow the steps that we discussed:
Step 1️⃣ Study the terms involved in the expression
Step 2️⃣ Rewrite terms to their common bases
Step 3️⃣ Activate the Laws of Indices
Keep on following our blog posts for more Secondary 3 A-Math tips!

If you like our methodology, we've some ongoing weekly Math classes:







